An interesting way to look at using something like derivatives to recover a function is in 3 categories.

In the first, are functions whose tail go to zero. This means that an arbitrarily finite number of terms is enough to uniformly get close to that function. These functions can be computed with Taylor series and converge everywhere

In the second category, are functions whose tails don't go to zero. These are functions with singularities, and but their tails can often be approximated using the information provided by the previous derivatives. Often, smoothing is enough to get these functions to converge, but other methods such as analytical continuation have the power to recover these functions

The final type of function is those whose derivatives don't provide information about their tails. In the extreme case, we have the derivatives all being zero yet the later derivatives are non-zero. If we look at e^(-1/x^2), we have that the derivatives are zero for all finite values but must eventually go to infinity in an arbitrarily small neighborhood around 0. This is due to the behavior of (-n)!, which can be seen by expanding the Taylor series of e^x, replacing x ith (-1/x^2), and switching n to -n using the rules of logarithmic integrals. I believe the best way to approximate these functions are to look at ways of handling infinity as if it were a smaller number and approximating in the right direction. One possible method is something like this: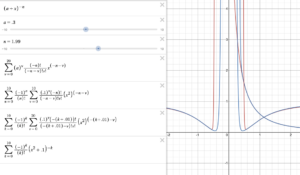

I'll look further into this, since I believe it holds the key to analytically continuing certain gap series, and maybe even all series with natural boundaries since most functions with natural boundaries should have a non-zero tail after infinity that isn't connected with its values before the tail.